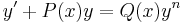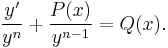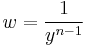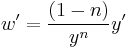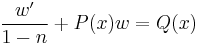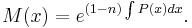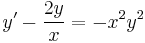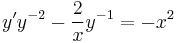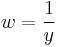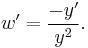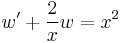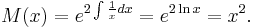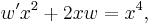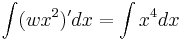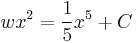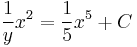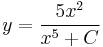Bernoulli differential equation

In mathematics, an ordinary differential equation of the form

$y'%2B P(x)y = Q(x)y^n\,$

is called a Bernoulli equation when n≠1, 0, which is named after Jakob Bernoulli, who discussed it in 1695 (Bernoulli 1695). Bernoulli equations are special because they are nonlinear differential equations with known exact solutions.

Contents

1 Solution
2 Example
3 References
4 External links

Solution

Dividing by 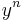$y^n$ yields

$\frac{y'}{y^{n}} %2B \frac{P(x)}{y^{n-1}} = Q(x).$

A change of variables is made to transform into a linear first-order differential equation.

$w=\frac{1}{y^{n-1}}$

$w'=\frac{(1-n)}{y^{n}}y'$

$\frac{w'}{1-n} %2B P(x)w = Q(x)$

The substituted equation can be solved using the integrating factor

$M(x)= e^{(1-n)\int P(x)dx}.$

Example

Consider the Bernoulli equation

$y' - \frac{2y}{x} = -x^2y^2$

We first notice that $y=0$ is a solution. Division by 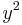$y^2$ yields

$y'y^{-2} - \frac{2}{x}y^{-1} = -x^2$

Changing variables gives the equations

$w = \frac{1}{y}$

$w' = \frac{-y'}{y^2}.$

$w' %2B \frac{2}{x}w = x^2$

which can be solved using the integrating factor

$M(x)= e^{2\int \frac{1}{x}dx} = e^{2\ln x} = x^2.$

Multiplying by 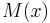$M(x)$ ,

$w'x^2 %2B 2xw = x^4,\,$

Note that left side is the derivative of 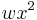$wx^2$ . Integrating both sides results in the equations

$\int (wx^2)' dx = \int x^4 dx$

$wx^2 = \frac{1}{5}x^5 %2B C$

$\frac{1}{y}x^2 = \frac{1}{5}x^5 %2B C$

The solution for $y$ is

$y = \frac{5x^2}{x^5 %2B C}$

as well as 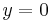$y=0$ .

Verifying using MATLAB symbolic toolbox by running

x = dsolve('Dy-2*y/x=-x^2*y^2','x')

gives both solutions:

0
x^2/(x^5/5 + C1)

also see a solution by WolframAlpha, where the trivial solution 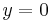$y=0$ is missing.

References

Bernoulli, Jacob (1695), "Explicationes, Annotationes & Additiones ad ea, quae in Actis sup. anni de Curva Elastica, Isochrona Paracentrica, & Velaria, hinc inde memorata, & paratim controversa legundur; ubi de Linea mediarum directionum, alliisque novis", Acta Eruditorum . Cited in Hairer, Nørsett & Wanner (1993).
Hairer, Ernst; Nørsett, Syvert Paul; Wanner, Gerhard (1993), Solving ordinary differential equations I: Nonstiff problems, Berlin, New York: Springer-Verlag, ISBN 978-3-540-56670-0 .

External links